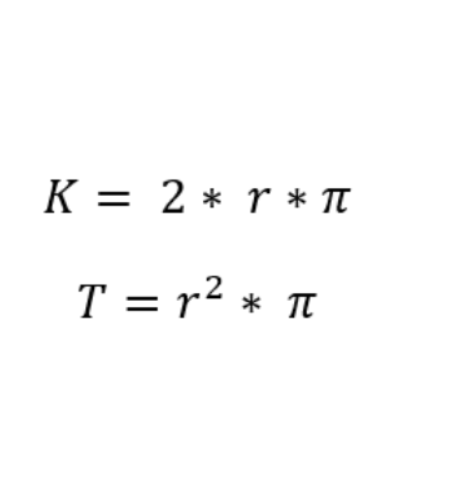A matematika egyik legizgalmasabb és leggyakrabban előforduló alakzata a kör, amely nem csak a mindennapi életünkben, hanem a tudományban és technikában is kiemelt szerepet játszik. Sokan találkoztak már azzal a feladattal, hogy ki kell számolni egy kör területét vagy kerületét, de nem mindig egyértelmű, hogyan is kezdjünk hozzá, illetve milyen adatokat kell ehhez ismernünk. Ez a cikk részletes és átfogó útmutatót nyújt mindazoknak, akik szeretnék megérteni a körrel kapcsolatos legfontosabb matematikai fogalmakat, illetve szeretnék magabiztosan kiszámítani egy kör területét és kerületét. Megismerjük a kör szerkezetét, megtanuljuk, hogyan használjuk fel a különböző adatokat a számítások során, és lépésről lépésre végigvezetjük az olvasót a teljes folyamaton. Emellett kitérünk a leggyakoribb hibákra is, amelyek a körrel kapcsolatos számítások során előfordulhatnak, és praktikus tanácsokat adunk ezek elkerülésére. Az útmutató nemcsak kezdőknek, hanem haladóknak is hasznos, hiszen a részletek feltárása révén mindenki elmélyítheti tudását. Különös hangsúlyt fektetünk a gyakorlati példákra, hogy az elmélet mellett a valós életben is könnyedén alkalmazható legyen a megszerzett tudás. Foglalkozunk a képletek eredetével, jelentőségével, és azzal is, hogy mikor, melyik változatot érdemes használni.
Legyen szó iskolai tanulásról, mérnöki feladatokról vagy egyszerűen csak kíváncsiságról, ebben az írásban mindenki megtalálja a számára hasznos információkat a kör területének és kerületének kiszámításához. Merüljünk el együtt a körök világában, és fejtsük meg, hogyan is működik ez az örök klasszikus forma!
A kör fogalma és legfontosabb jellemzői
A kör egy síkbeli, szabályos, zárt görbe, amelynek minden pontja egy adott ponttól—az úgynevezett középponttól—ugyanakkora távolságra van. Ez az állandó távolság a kör sugara (jele: r). Ezt úgy is elképzelhetjük, mintha egy ceruzával egy fonalat, amely egyik végével rögzítve van, körbevezetnénk: a ceruza által húzott vonal a kör, a fonal hossza pedig a sugár.
A körnek van még egy fontos tulajdonsága: az átmérő (jele: d), amely a kör két legtávolabbi pontját összekötő szakasz, és átmegy a középponton. Az átmérő hossza mindig kétszerese a sugárnak (d = 2r). A körhöz kapcsolódik még a kerület (azaz a teljes „vonalhossz”) és a terület (azaz a körön belüli sík egy része). A kör minden irányból szimmetrikus, nincsenek kiemelt pontjai vagy irányai, ami miatt az egyik legkülönlegesebb alakzat a geometriában.
A körrel kapcsolatos matematikai fogalmak már az ókori civilizációkban is megjelentek: a görögök, egyiptomiak és babilóniaiak is alkalmazták őket az építészetben, földmérésben és más tudományokban. A körhöz kötődő egyik legismertebb állandó a „pí” (π), amely a kör kerületének és átmérőjének arányát fejezi ki. Ez az irracionális szám (körülbelül 3,14159) alapvető szerepet tölt be a körrel kapcsolatos számításokban.
A kör szerkezete tehát néhány egyszerű, mégis nagyon fontos elemből áll. A középpont, a sugár, az átmérő, a kerület és a terület mind hozzájárulnak ahhoz, hogy pontosan meghatározhassuk a kör méretét és tulajdonságait. Ezeknek az elemeknek a megértése nélkülözhetetlen a további számításokhoz és a körrel kapcsolatos feladatok magabiztos kezeléséhez.
Milyen adatok szükségesek a számításhoz?
Ahhoz, hogy egy kör kerületét és területét meghatározhassuk, szükségünk van legalább egy alapvető adatra: a kör sugarára vagy átmérőjére. Ezek közül bármelyik ismeretében már elvégezhetjük a szükséges számításokat, mert a két adat között szoros összefüggés van. A sugár (r) és az átmérő (d) közötti kapcsolat: d = 2r vagy fordítva, r = d / 2.
Természetesen előfordulhat, hogy a feladatban nem közvetlenül a sugár vagy az átmérő, hanem például a kör kerülete vagy területe ismert, és ebből kell visszakövetkeztetnünk a másik adatra. Ilyenkor a képleteket kell átalakítanunk a kívánt ismeretlen kifejezésére. Az alábbi táblázat összefoglalja, mely adatokból milyen következtetések vonhatók le:
| Ismert adat | Képlet | Meghatározható adatok |
|---|---|---|
| Sugár (r) | d = 2r | Átmérő, Kerület, Terület |
| Átmérő (d) | r = d / 2 | Sugár, Kerület, Terület |
| Kerület (K) | r = K / (2π) | Sugár, Átmérő, Terület |
| Terület (T) | r = √(T/π) | Sugár, Átmérő, Kerület |
Az adatok pontos ismerete kulcsfontosságú, mert minden további számítás ebből indul ki. Ha például egy kerek asztal terítőjét szeretnénk kiszabni, elég lehet csak a sugár hossza, de ha egy körpályát szeretnénk végigfutni, akkor inkább a kerület az érdekes számunkra. Ezért érdemes először mindig azt tisztázni, milyen adat áll rendelkezésünkre, és mire van szükségünk.
A gyakorlati életben legtöbbször a sugár vagy az átmérő mérhető meg egyszerűen, például egy kör alakú tárgy (mint egy tányér vagy egy pénzérme) középpontjától a széléig mérve. Ha mégis a kerület vagy terület mérhető (például egy kör alakú kert körbekerítésekor), akkor ezekből is vissza lehet számolni a szükséges adatokat, és elvégezni a többi számítást. Ezért a képletek helyes ismerete és alkalmazása elengedhetetlen.
A kör kerületének kiszámítása lépésről lépésre
A kör kerülete azt mutatja meg, milyen hosszú lenne a körvonal, ha „kikötnénk” és egy egyenes szakaszra fektetnénk. A kerület (K) számítása szorosan kötődik a sugarához vagy átmérőjéhez, valamint a π (pí) nevű matematikai állandóhoz. A leggyakrabban használt képlet a következő:
K = 2 × π × r
ahol K a kör kerülete, r a sugár, π pedig körülbelül 3,1416.
Ha az átmérő ismert, akkor a képlet egyszerűbb:
K = π × d
ahol d az átmérő.
Vegyünk egy konkrét példát: Tegyük fel, hogy egy játszótéren található kör alakú homokozó sugara 2,5 méter. A kerület kiszámításához helyettesítsük be a számokat:
K = 2 × π × 2,5 ≈ 2 × 3,1416 × 2,5 ≈ 15,708 méter.
Ez azt jelenti, hogy ha a homokozót körbe szeretnénk keríteni, körülbelül 15,7 méter hosszú kerítésre lesz szükségünk.
Ha az átmérő áll rendelkezésünkre, például egy kör alakú asztal átmérője 1,2 méter, a kerület:
K = π × 1,2 ≈ 3,1416 × 1,2 ≈ 3,77 méter.
Ez jól mutatja, hogy bármelyik adatból egyszerűen számítható a kerület, csak a megfelelő képletet kell alkalmazni.
A kerület számítása gyakran előfordul a mindennapi életben: például ha egy kör alakú virágágyást szeretnénk körbeszegni, vagy ha egy kerékpár kereke hányszor fordul meg egy adott távolság alatt. A képletek alkalmazását megkönnyíti, hogy a π értéke mindig adott, és a sugár vagy átmérő mérése sem bonyolult.
Érdemes megjegyezni, hogy a pontos számításokhoz a π minél több tizedesjegyét használjuk, de a legtöbb gyakorlati feladathoz elegendő a 3,14 vagy 3,1416 érték. Az iskolai feladatokban általában megadják, milyen pontossággal számoljunk, de a mindennapokban a kerekített érték is megteszi.
A kör területének meghatározása egyszerűen
A kör területe (T) azt fejezi ki, hogy mekkora síkbeli részt foglal el a kör. Más szóval, ez az a „hely”, amelyet a körvonalon belül találunk. A leggyakrabban használt képlet a következő:
T = π × r²
ahol T a terület, r a sugár.
Ez azt jelenti, hogy a sugár négyzetét megszorozzuk a π értékével. A képlet értelmezése egyszerű: ha a sugár hosszát négyzetre emeljük, egy „négyzetnyi” területet kapunk, amit a π konstanssal megszorozva megkapjuk a kör síkbeli területét.
Vegyünk egy példát: Egy kör alakú tó sugara 7 méter. A terület kiszámítása:
T = π × 7² = π × 49 ≈ 3,1416 × 49 ≈ 153,9384 m².
Ez azt jelenti, hogy a tó vízfelülete körülbelül 154 négyzetméter.
Ha az átmérő ismert, a sugár meghatározása után használjuk ugyanazt a képletet:
Például, ha egy kör alakú kert átmérője 12 méter, a sugár r = 12 / 2 = 6 méter.
T = π × 6² = π × 36 ≈ 113,0976 m².
A kör területének kiszámítása különösen hasznos lehet földmérésnél, kerttervezésnél, de akár lakberendezésnél vagy ipari tervezésnél is. Gyakran előfordulhat, hogy egy adott területű kör alakú helyet kell kialakítani vagy beépíteni, például egy kör alakú szökőkút vagy medence esetében.
Fontos tudni, hogy a terület számításánál is célszerű a π megfelelő pontosságát használni, a feladat jellege szerint. A négyzetre emelés (r²) mindig első lépés, utána következik a szorzás a π értékével. Ez biztosítja az egyszerű és gyors számítást, amelyhez csak egy alapműveletet kell elvégezni.
Gyakori hibák a körrel kapcsolatos számításokban
Annak ellenére, hogy a kör kerületének és területének számítása látszólag egyszerű, rengeteg apró hiba csúszhat a számításokba, amelyek elkerülhetők egy kis odafigyeléssel. Az egyik leggyakoribb hiba, hogy összekeverik a sugár és az átmérő fogalmát. Sokszor előfordul, hogy a megadott adat az átmérő, de a képletben a sugárral kell dolgozni, ilyenkor elfelejtik elosztani kettővel az átmérőt, és hibás eredmény születik.
Másik gyakori hiba a π értékének helytelen használata. Sokszor túlzottan kerekítenek (például 3-at vagy 3,1-et használnak), ami főleg nagyobb méreteknél jelentős eltérést okozhat a végeredményben. Javasolt mindig legalább 3,14-et, de még inkább 3,1416-ot használni, ha pontos eredményt szeretnénk kapni.
Szintén tipikus probléma, hogy a négyzetre emelést rosszul végzik el, például csak kétszeres szorzást végeznek, ahelyett hogy r × r-t számolnának. Az átmérő esetében is sokszor előfordul, hogy nem számolják át sugárrá, és így hibás területet vagy kerületet kapnak.
Egy másik elterjedt hiba, hogy nem egységes mértékegységekkel dolgoznak. Például, ha a sugár centiméterben adott, a területet pedig négyzetméterben kell megadni, elfelejtik átváltani a mértékegységeket, ami szintén rossz eredményhez vezethet. Fontos, hogy minden adatot ugyanabban a mértékegységben használjunk a számítás során.
A hibák elkerülése érdekében mindig ellenőrizzük, milyen adatokat kaptunk, melyik képletet kell alkalmazni, és használjunk pontos értékeket mind a sugár, mind a π tekintetében. Célszerű a számítás minden lépését világosan levezetni, hogy könnyen átlátható legyen, hol esetleges a hiba lehetősége.
Előnyök és hátrányok: Mikor érdemes kör alakzatot választani?
A kör mint forma számos előnnyel jár, mind esztétikai, mind funkcionális szempontból. Az egyik legnagyobb előnye, hogy a kör minden pontja egyenlő távolságra van a középponttól, ami ideálissá teszi például tartályok, kutak, vagy akár asztalok kialakításánál. A kör alakzat emellett könnyen kezelhető matematikailag, hiszen csak egyetlen adat (a sugár vagy átmérő) és egy állandó (π) szükséges a legtöbb számításhoz.
Azonban vannak hátrányai is: a kör alakú terület például nehezen osztható fel szabályos részekre, és a körvonal mentén történő „illesztések” (például burkolólapok fektetése) bonyolultabb, mint egy négyszög esetén. Ezen kívül a tárolás vagy szállítás során a kör alakú tárgyak több „üres helyet” hagyhatnak maga körül, mint a négyzet vagy téglalap alakúak.
Az alábbi táblázat összefoglalja a kör alakzat használatának előnyeit és hátrányait:
| Előnyök | Hátrányok |
|---|---|
| Egyszerű számítások (csak sugár + π) | Nehezen illeszthető más alakzatokhoz |
| Esztétikus, szimmetrikus forma | Felosztása, beépítése bonyolult lehet |
| Ideális tartályok, edények kialakításához | Tárolásnál, szállításnál helypazarlóbb |
| Minden oldalról egyforma távolságú középpont | Burkolás, szegélyezés komplikáltabb |
Döntésnél tehát érdemes mérlegelni, hogy a kör mely előnyeit szeretnénk kihasználni, illetve a hátrányokat mennyire tudjuk kezelni a tervezés során.
Összefoglalás: Mire figyeljünk a körrel kapcsolatos számítások során?
A kör kerületének és területének számítása tehát nemcsak matematikaórán, de a mindennapi életben is fontos és hasznos tudás. A legfontosabb, hogy mindig tisztában legyünk a rendelkezésünkre álló adatokkal, helyesen használjuk a képleteket, és fordítsunk figyelmet a mértékegységek egyezőségére.
A gyakorlati példák azt mutatják, hogy a kör kerületének és területének meghatározása egyszerű, ha helyesen alkalmazzuk a tanultakat. Mindig ellenőrizzük, hogy sugárral vagy átmérővel dolgozunk, és ügyeljünk a π értékére. Ha ezekre a részletekre odafigyelünk, biztosan helyes eredményeket kapunk, akár egy kör alakú kert, akár egy körpálya, akár egy új asztalterítő esetében.
A körrel kapcsolatos matematikai ismeretek mindenki számára hasznosak lehetnek, nemcsak az iskolában, hanem a mindennapokban is. Legyen szó egy egyszerű felmérésről, építkezésről vagy akár hobbi barkácsolásról, a kör kerületének és területének kiszámítása alapvető tudás. Reméljük, hogy ez a részletes útmutató segített abban, hogy magabiztosan és hibamentesen végezd el a szükséges számításokat, és hogy tisztábban lásd a kör különleges világát. Ne feledd: a precíz számítás alapja a pontos adatok, a helyes képlet és egy kis figyelem! Ha pedig elakadnál, nyugodtan keresd fel ezt az írást ismét, vagy nézd át a gyakran ismételt kérdéseket a végén!
GYIK – Gyakran ismételt kérdések
Mi a kör sugara és hogyan mérhetem meg?
A kör sugara a középponttól a körvonal bármely pontjáig mért távolság. Egy vonalzóval vagy mérőszalaggal megmérheted, ha a középpontot megtalálod.Mi az átmérő és hogyan számolom ki a sugárból?
Az átmérő a kör két legtávolabbi pontja közötti szakasz, amely áthalad a középponton. Kiszámítása: d = 2r.Mi az a π (pí), és miért használjuk?
A π egy matematikai állandó, amely a kör kerületének és átmérőjének aránya (kb. 3,1416). Nélküle nem lehet pontosan kiszámolni kerületet vagy területet.Mi a különbség a kerület és a terület között?
A kerület a körvonal hossza, míg a terület a körön belüli „hely” (síkbeli rész).Hogyan tudom kiszámítani egy kör területét, ha csak az átmérőt ismerem?
Előbb oszd el az átmérőt kettővel (így megkapod a sugarat), majd a képlettel (T = π × r²) határozd meg a területet.Mi a leggyakoribb hiba a számítások során?
Leggyakrabban a sugár és átmérő összekeverése, illetve a mértékegységek elhanyagolása okoz problémát.Milyen gyakorlati területeken fontos a kör kerülete és területe?
Földmérés, asztalosmunka, kertépítés, ipar, építészet, sportpálya tervezés stb.Mennyi legyen a π értéke a számításokhoz?
Általában elég a 3,14 vagy 3,1416, de tudományos számításoknál lehet több tizedesjegyet is használni.Melyik képletet használjam, ha a kör kerületét szeretném tudni?
Ha ismered a sugarat: K = 2 × π × r; ha az átmérőt: K = π × d.Mit tegyek, ha csak a kerületet ismerem, de a terület kell?
Először számold ki a sugarat: r = K / (2π), majd a területet: T = π × r².
- Olvasónaplók
- Verselemzések
- Történelem érdekességek
- Matematikai érdekességek
- Mértékegység átváltás
- Fizika érdekességek
- Biológia érdekességek
- Irodalmi érdelességek
- Mikor volt?
- Kik voltak?
- Ki találta fel
- Magyarország lakosága
- Mikor kell-hogyan kell-miért kell
- Matek infó
- Bizony-bizony
- Tudtad?
- Szavak jelentése
- Olvasónaplóm