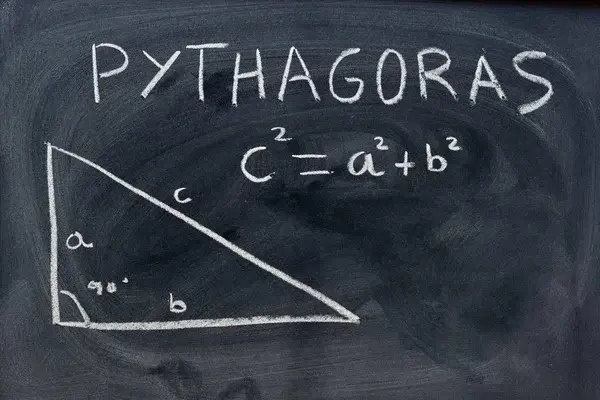Hogyan számoljuk ki a pitagoraszi tételt? Sokan találkoznak ezzel a matematikai tétellel már általános iskolában, de gyakran felmerül a kérdés: pontosan mire való, és hogyan is kell kiszámolni? Ebben a cikkben részletesen bemutatjuk, mi is az a pitagoraszi tétel, hogyan lehet alkalmazni hétköznapi helyzetekben, és mit jelentenek a háromszög oldalainak betűi. Megnézzük, hogyan lehet lépésről lépésre elvégezni a számításokat, elkerülve a leggyakoribb hibákat. Az útmutató hasznos lesz kezdőknek, de azoknak is, akik már gyakorlottabban használják ezt a tételt, de szeretnék felfrissíteni tudásukat. Konkrét, számokkal illusztrált példát is megoldunk, hogy világos és követhető legyen minden lépés. Külön kitérünk azokra a tippekre, amelyek megkönnyítik a helyes számolást, és egy táblázatban összegezzük a legfontosabb előnyöket és hátrányokat. A végén egy 10 pontos GYIK segít még jobban eligazodni a témában. Célunk, hogy mindenki magabiztosan tudja használni a pitagoraszi tételt a mindennapi életben vagy a tanulmányai során. Vágjunk is bele a részletekbe!
Mi az a pitagoraszi tétel és mire használható?
A pitagoraszi tétel egyike a legismertebb geometriai tételeknek, melyet az ókori görög matematikus, Pitagorasz nevéhez kötünk. Ez a tétel kijelenti, hogy minden derékszögű háromszögben a két befogó négyzetének összege egyenlő az átfogó négyzetével. Matematikai szimbólumokkal így írjuk le: a² + b² = c², ahol a és b a háromszög két rövidebb oldala (befogók), c pedig a leghosszabb oldal, azaz az átfogó.
A pitagoraszi tétel számos területen gyakorlati jelentőséggel bír. Használjuk például építkezésnél, amikor pontosan kell kiszámolni egy tető lejtését vagy a szoba átlóját. Segítségével meghatározhatjuk két pont közötti távolságot, ha azok derékszögű koordinátarendszerben helyezkednek el. Fontos hangsúlyozni, hogy a tétel kizárólag derékszögű háromszögekre alkalmazható, így mindig ellenőrizni kell, hogy valóban ilyen háromszöggel van-e dolgunk.
A háromszög oldalainak elnevezése és jelentése
A derékszögű háromszöget három oldal határolja, melyeket speciális neveken emlegetünk. A két rövidebb oldalt befogónak hívjuk, ezeket általában a és b betűvel jelöljük a képletekben. A harmadik, egyben leghosszabb oldal az átfogó, mely a derékszöggel szemben helyezkedik el, ezt c-vel jelöljük. Ez a háromszög azon oldala, amely összeköti a két befogó végét.
Az oldalak elnevezése nem önkényes, hanem a tétel alkalmazása szempontjából kulcsfontosságú. A pitagoraszi tétel csak akkor működik helyesen, ha megfelelően azonosítjuk a befogókat és az átfogót. Az egyik leggyakoribb hiba, hogy véletlenül összekeverjük az oldalakat, ezért mindig nézzük meg, melyik szög a derékszög, és ehhez képest nevezzük el az oldalakat. Például ha egy háromszögben az egyik szög 90°, akkor az ezzel szemben lévő oldal lesz az átfogó.
Lépésről lépésre: a pitagoraszi tétel képlete
A pitagoraszi tétel alkalmazása lépésről lépésre történik. Először is, bizonyosodjunk meg róla, hogy valóban derékszögű háromszögről van szó! Ezután azonosítsuk a három oldal közül az átfogót és a két befogót. A képlet: a² + b² = c². Ez azt jelenti, hogy a két befogó hosszát négyzetre emeljük, majd összeadjuk, az eredmény pedig az átfogó hosszának négyzete lesz.
Ha szeretnénk meghatározni valamelyik ismeretlen oldalt, például az átfogót (c), akkor a következő lépéseket kell követni:
- Négyzetre emeljük az ismert befogók hosszát.
- Összeadjuk ezeket az értékeket.
- A végeredményből négyzetgyököt vonunk, hogy megkapjuk az átfogó hosszát.
Példa egyértelmű számokkal:
- Ha a = 3 és b = 4, akkor c = √(3² + 4²) = √(9 + 16) = √25 = 5.
Példa feladat: számoljuk ki az átfogót együtt!
Tegyük fel, hogy adott egy derékszögű háromszög, ahol az egyik befogó (a) hossza 6 cm, a másik befogó (b) pedig 8 cm. Az a kérdés, hogy mekkora az átfogó (c) hossza? Alkalmazzuk a pitagoraszi tétel lépéseit:
Első lépés: Négyzetre emeljük a befogók hosszát:
6² = 36,
8² = 64.Második lépés: Összeadjuk az eredményeket:
36 + 64 = 100.
Harmadik lépés: Négyzetgyököt vonunk az összegből:
√100 = 10.
Így az átfogó hossza 10 cm. Ez a módszer minden, derékszögű háromszög esetén alkalmazható, ha legalább két oldal hosszát ismerjük. Nézzünk egy táblázatot, amely összefoglalja, mikor melyik oldalt számoljuk:
| Ismert adatok | Képlet, amit használunk | Mit kapunk meg? |
|---|---|---|
| a, b | c = √(a² + b²) | Átfogó (c) |
| c, a | b = √(c² – a²) | Befogó (b) |
| c, b | a = √(c² – b²) | Befogó (a) |
Tippek és gyakori hibák a számítás során
Tippek a helyes számításhoz:
- Mindig győződjünk meg arról, hogy valóban derékszögű háromszögről van-e szó!
- Ügyeljünk az oldalak helyes azonosítására: csak a derékszöggel szemben lévő oldal lehet az átfogó.
- Ha nem egész számot kapunk, a végeredményt kerekítsük a kívánt tizedesjegyre.
- Használjunk számológépet a négyzetgyök pontos meghatározásához.
Gyakori hibák:
- Az oldalak összekeverése, vagyis a befogó helyett az átfogó négyzetének beszámítása a rossz oldalhoz.
- Nem derékszögű háromszögre próbálják alkalmazni a tételt.
- Elfelejtik négyzetgyököt vonni a végén, így az eredményt négyzetben hagyják.
- Rossz sorrendben vonnak össze vagy végeznek műveleteket, ami hibás eredményhez vezet.
Előnyök és hátrányok táblázata:
| Előnyök | Hátrányok |
|---|---|
| Könnyen alkalmazható, gyors | Csak derékszögű háromszögnél használható |
| Átlós távolság számítására ideális | Csak síkban érvényes, térben módosul |
| Sok területen, pl. építészetben hasznos | Oldalak helytelen megjelölése hibás eredményt adhat |
| Ismeretlen oldal meghatározása egyszerű | Tizedes eredményeknél kerekíteni kell |
GYIK – Gyakran ismételt kérdések
Mi az a pitagoraszi tétel lényege?
A derékszögű háromszög két rövidebb oldalának négyzetösszege megegyezik a leghosszabb oldal (átfogó) négyzetével.Mikor használhatom a pitagoraszi tételt?
Csak derékszögű háromszögek esetén alkalmazható.Mire jó a pitagoraszi tétel a mindennapokban?
Használható távolságmérésre, építészetben, vagy bármilyen helyzetben, ahol két merőleges oldal és az átló összefüggése érdekes.
Honnan tudom, melyik az átfogó?
Az átfogó mindig a derékszöggel szemben lévő, leghosszabb oldal.Mi a teendő, ha nem egész számot kapok a végeredményre?
Kerekítsd a végeredményt a kívánt tizedesjegyre.Alkalmazható a tétel háromdimenziós (térbeli) alakzatokra?
Csak síkban, a térbeli kiterjesztéshez a tétel általánosítását (térbeli pitagoraszi tétel) kell használni.Mi történik, ha felcserélem a befogókat?
Nem történik semmi, mert a sorrend nem számít – a lényeg, hogy az átfogó a helyén legyen.Hogyan ellenőrizhetem, hogy derékszögű a háromszög?
Ha a három oldal ismert, ellenőrizd, hogy teljesül-e az a² + b² = c² összefüggés.Lehet-e az átfogót megtalálni, ha csak egy oldalt ismerek?
Nem, legalább két oldal hosszát kell ismerni a számításhoz.Milyen hibalehetőségek vannak a számítás közben?
Gyakori, hogy rossz oldalakat választanak, elfelejtik a négyzetgyököt, vagy nem derékszögű háromszögnél alkalmazzák a tételt.
Reméljük, ezzel a cikkel sikerült közelebb hozni a pitagoraszi tétel világát, hogy magabiztosan használhasd bármikor, amikor szükség van rá!