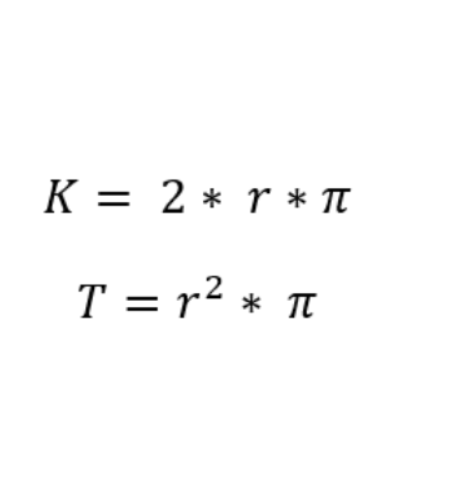Matematika érdekességek

Hogyan számoljuk ki a súlypontot egy alakzatban?

Olvasónaplók, verselemzések2 óra ezelőtt031 perc

A matematika és a fizika világában a súlypont fogalma egyike azoknak az alapvető témáknak, amelyek nélkülözhetetlenek a mindennapi élet számos területén. A mérnöki tervezéstől kezdve, az építőiparon át, egészen a művészi kompozíciókig, a súlypont meghatározása létfontosságú tudás. E cikk célja, hogy alaposan bemutassa, hogyan számoljuk ki a súlypontot különböző alakzatokban, legyen szó egyszerű vagy összetettebb formákról. Megvizsgáljuk, hogy miért olyan fontos a súlypont, milyen alapfogalmak szükségesek a megértéséhez, és milyen módszerekkel lehet pontosan meghatározni. A kezdők gyakran találkoznak kihívásokkal ezen a területen, ezért részletes, szemléletes példákkal és magyarázatokkal segítünk elmélyíteni a tudást. Azok számára is tartogatunk újdonságokat, akik már jártasak a matematikai számításokban, hiszen a bonyolultabb alakzatok súlypontjának meghatározása is terítékre kerül. A mindennapi praktikusság érdekében gyakorlati tippekkel, valamint a leggyakoribb hibák felsorolásával is készülünk. Egy átfogó táblázat segítségével az előnyöket és hátrányokat is összevetjük, hogy átláthatóbbá váljon az egyes módszerek alkalmazhatósága. Végül egy átfogó GYIK (Gyakran Ismételt Kérdések) részben válaszolunk a legfontosabb felmerülő kérdésekre, hogy mindenki magabiztosan használhassa ezt a tudást a jövőben.

Mi az a súlypont, és miért fontos az alakzatoknál?

A súlypont (más néven tömegközéppont vagy centrioid) egy adott alakzat vagy test azon pontja, amely körül a súly vagy a tömeg egyenletesen oszlik el. Ez a pont olyan, mintha az egész alakzat vagy test összes tömege, súlya ebben az egyetlen pontban koncentrálódna. A síkbeli és térbeli alakzatoknál egyaránt meghatározható a súlypont, és minden testnek csak egyetlen súlypontja van. Például egy szabályos háromszög esetén a súlypont a három csúcsot összekötő szakaszok metszéspontja.

A súlypont ismerete nemcsak elméleti szempontból hasznos; a gyakorlatban is kritikus szerepet játszik. Gondoljunk bele egyensúlyozási feladatokba, például egyensúlyozni egy vonalzót az ujjunkkal. Ha pontosan a súlypontjához helyezzük az ujjunkat, akkor az nem fog elbillenni egyik irányba sem. Ugyanez az elv érvényesül nagyobb léptékben is – legyen szó hidak, épületek, járművek vagy akár műalkotások tervezéséről. Ha nem jól határozzuk meg a súlypontot, az súlyos problémákhoz vezethet; például egy rosszul kiegyensúlyozott szerkezet könnyen felborulhat vagy összedőlhet. Éppen ezért a súlypont számítása minden mérnök, építész, fizikus – de akár művész számára is alapvető fontosságú.

Alapfogalmak: súlypont számításának kiindulópontjai

A súlypont számításához először is tisztában kell lennünk néhány alapvető fogalommal. A legfontosabb ezek közül a koordináta-rendszer használata, amelyben az adott alakzatot elhelyezzük. A koordináta-rendszer lehet kétdimenziós (síkbeli) vagy háromdimenziós (térbeli), attól függően, hogy milyen testtel dolgozunk. Például a síkbeli alakzatoknál az (x, y) koordinátákat használjuk, míg térbeli testeknél az (x, y, z) koordinátákat.

Második fontos fogalom az alakzat tömege vagy területe. A tömegközéppont meghatározásához ugyanis tudnunk kell, hogy az adott test milyen tömegeloszlással rendelkezik. Ha az alakzat homogén anyagból készült (vagyis mindenhol azonos a sűrűsége), akkor a súlypont számítása egyszerűbb, hiszen elég csak a terület vagy a térfogat alapján számolni. Nem homogén testeknél azonban bonyolultabb a helyzet, ott figyelembe kell venni minden egyes rész tömegét és elhelyezkedését is.

Ezek után következik a rész-alakzatok fogalma, amely azt jelenti, hogy egy bonyolultabb testet több egyszerűbb alakzatra bonthatunk. Így minden egyes részre külön-külön meghatározható a súlypont, és ezek összességéből kiszámítható a teljes test súlypontja. Ez a módszer főleg akkor hasznos, ha az alakzat nem szabályos, vagy ha több különböző anyagból készült. Itt lép be az úgynevezett súlyozott átlag fogalma is, amely a rész-alakzatok tömegének arányában számolja át a teljes test súlypontját.

A súlypont kiszámítása tehát matematikailag úgy történik, hogy a részek súlypontjait az azokhoz tartozó tömegekkel vagy területekkel súlyozva átlagoljuk. Például, ha két részünk van, az egyik tömege 3 kg, a másik 2 kg, akkor a súlypont a nagyobb tömeghez közelebb fog esni. Ez a módszer lehetővé teszi, hogy összetett alakzatok esetén is pontosan meghatározzuk a súlypontot, ami kulcsfontosságú a stabilitás és az egyensúly szempontjából.

Egyszerűbb alakzatok súlypontjának meghatározása

Kezdjük a leggyakrabban előforduló síkbeli, egyszerűbb alakzatokkal. Ezek, mint például a négyzet, téglalap, kör vagy háromszög, a legkézenfekvőbbek, és szerencsére a súlypontjuk is könnyen meghatározható. Ezeknél jellemzően a szimmetria lehetővé teszi, hogy ránézésre is megsejtsük, hol található a súlypont.

Vegyük például a téglalapot. Ha a téglalap sarkait (0,0), (a,0), (a,b) és (0,b) koordinátákkal jelöljük, akkor a súlypontja az átlók metszéspontja, amely az (a/2, b/2) pontban van. A kör esetén – akármekkora is legyen – a súlypontja mindig a középpont, vagyis ha a kör középpontja (x₀, y₀), akkor a súlypont is ott van. Ezeknél az alakzatoknál a középponti szimmetria miatt a súlypont meghatározása roppant egyszerű.

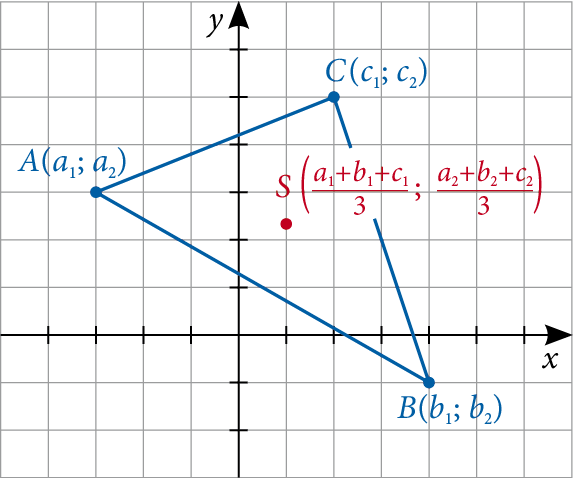
A háromszög esetében a helyzet kissé bonyolultabb, de szintén könnyen megérthető. A háromszög súlypontja az a pont, ahol a három súlyvonal (a csúcsokat az ellentétes oldalak felezőpontjával összekötő egyenesek) metszik egymást. Matematikailag, ha a háromszög csúcsai (x₁, y₁), (x₂, y₂) és (x₃, y₃), akkor a súlypont koordinátái:

x_s = (x₁ + x₂ + x₃) / 3
y_s = (y₁ + y₂ + y₃) / 3

Ez azt jelenti, hogy a háromszög minden csúcsától egyenlő távolságban helyezkedik el a súlypont. Például egy (0,0), (6,0), (3,6) csúcsokkal rendelkező háromszög súlypontja:

x_s = (0+6+3)/3 = 3
y_s = (0+0+6)/3 = 2

Így a súlypont a (3,2) koordinátán található.

Az egyszerűbb testek, például a kocka vagy téglatest esetén a súlypont a test középpontjában található. Egy téglatest, amelynek csúcsai (0,0,0) és (a,b,c), a súlypont az (a/2, b/2, c/2) pontba esik. Ezek az alapvető szabályok adnak kiindulási alapot a bonyolultabb formák vizsgálatához.

Összefoglaló táblázat: Egyszerű alakzatok súlypontja

Alakzat	Súlypont meghatározása	Képlet/Koordináta
Téglalap	Két átló metszéspontja	(a/2, b/2)
Kör	Középpont	(x₀, y₀)
Háromszög	Súlyvonalak metszéspontja	((x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3)
Téglatest	Test középpontja	(a/2, b/2, c/2)
Sáv (pl. rúd)	Középpont	(hossz/2, 0) (ha vízszintes)

Mint látható, az egyszerűbb alakzatoknál a szimmetria és az elhelyezkedés alapján viszonylag gyorsan meghatározhatjuk a súlypont helyét anélkül, hogy bonyolult számításokra lenne szükség.

Összetettebb alakzatok súlypontjának kiszámítása

A gyakorlatban azonban gyakran találkozunk összetett alakzatokkal, amelyek több egyszerűbb alakzatból állnak össze, vagy akár szabálytalanok is lehetnek. Ezeknél a súlypont meghatározása már részletesebb számítást igényel. Ilyenkor alkalmazzuk a rész-alakzatos módszert, amikor az összetett testet felbontjuk kisebb, egyszerűbb részekre, amelyek súlypontját már ismerjük vagy könnyen kiszámíthatjuk.

Tegyük fel, hogy van egy „L” alakú testünk, amely két, egymásra merőleges téglalapból áll. Az első téglalap mérete 4×2 cm, a másodiké 2×3 cm, amely az előzővel egy oldal mentén érintkezik, így együtt alkotják az „L” formát. Az ilyen alakzat súlypontját úgy határozhatjuk meg, hogy:

Kiszámoljuk mindkét rész területét (A₁=8 cm², A₂=6 cm²).
Meghatározzuk a két rész súlypontjának koordinátáit (legyenek (x₁, y₁) és (x₂, y₂)).
Ezután alkalmazzuk a súlyozott átlag képletét:
- x_s = (A₁×x₁ + A₂×x₂) / (A₁ + A₂)
- y_s = (A₁×y₁ + A₂×y₂) / (A₁ + A₂)

Ez a módszer természetesen bármennyi rész-alakzatra kiterjeszthető. Például, ha egy lapos, homogén anyagból készült testünk több szabályos formából áll, mindegyikhez meghatározzuk a súlypontot és a területet, majd ezek átlagát vesszük a teljes testre vonatkoztatva.

Másik gyakori eset a lyukas (kivágott) alakzatok, például egy négyzetből kivágott kör, ahol a kivágott részt negatív területként kezeljük. Ilyenkor a kivágott rész tömegét (területét) levonjuk az összegből, és a súlypont meghatározásánál is figyelembe vesszük ezt az irányt.

Példa: Negatív rész kezelése

Tegyük fel, hogy van egy 10×10 cm-es négyzetünk, amelynek közepéből egy 4 cm átmérőjű kör van kivágva.

A négyzet területe: A₁ = 100 cm², súlypontja a (5,5) pont.
A kör területe: A₂ = π×2² ≈ 12,57 cm², súlypontja szintén a (5,5) pont (hiszen középen van).

A teljes test súlypontja:

x_s = (A₁×x₁ − A₂×x₂) / (A₁ − A₂) = (100×5 − 12,57×5) / (100 − 12,57) ≈ (500−62,85)/87,43 ≈ 5
y_s = hasonlóan 5

Mivel mindkettő középen van, a súlypont nem változott, de ha a kivágott kör nem középre esik, akkor eltolódik a súlypont, ezt ezzel a módszerrel könnyen kiszámolhatjuk.

Folytonos alakzatok: Integrálás módszere

Ha az alakzat annyira összetett, hogy nem bontható egyszerű részekre, vagy a tömeg eloszlása nem egyenletes, akkor integrálásos módszert kell alkalmazni. Ilyenkor a teljes testet végtelenül sok pici, elemi részre bontjuk, majd ezek súlypontjának átlagát számítjuk ki:

x_s = (∫A x dA) / (∫A dA)

Ahol dA egy kis elem területe, x annak x koordinátája. Ez már haladóbb matematikai tudást igényel, de lehetővé teszi, hogy akár bonyolult görbékkel határolt alakzatok súlypontját is meghatározzuk.

Előnyök és hátrányok különböző módszereknél

Módszer	Előnyök	Hátrányok
Szemléltetés (szabályos alakzatok)	Gyors, egyszerű, könnyen ellenőrizhető	Csak szimmetrikus alakzatokra alkalmazható
Rész-alakzatos módszer	Alkalmas összetett, de szabályos alakzatokra	Sok számítást igényel, könnyű elrontani
Integrálás	A legpontosabb, bármilyen alakzatra alkalmazható	Matematikailag bonyolult, speciális eszközöket igényel

Összegezve, a választott módszer mindig az alakzat bonyolultságától, adott esetben a szükséges pontosságtól függ.

Gyakori hibák és tippek a súlypont számításához

A súlypont meghatározásánál számos hibaforrás merülhet fel, különösen bonyolultabb alakzatoknál. Az egyik leggyakoribb hiba, hogy rosszul választjuk meg a koordináta-rendszert. Ha az origó nem megfelelő helyen van, az egész számítás hibás lesz, ezért mindig gondoljuk át, honnan mérjük a távolságokat!

Másik gyakori hiba a rész-alakzatok elhelyezkedésének és területének téves meghatározása. Előfordul, hogy elfelejtjük levonni a kivágott részeket, vagy rosszul számoljuk ki a területeket, tömegeket, így a súlypont is hibásan alakul. Ezért érdemes minden részelemet külön-külön is ellenőrizni, hogy biztosan helyesek-e a számok.

Az is előfordulhat, hogy a súlypont helyét vizuálisan rosszul becsüljük meg. Ezért érdemes mindig vázlatot, rajzot készíteni az alakzatról, és bejelölni a részek súlypontjait, hogy könnyebben áttekinthető legyen az egész test szerkezete. Praktikus trükk, hogy a súlypont mindig a nagyobb tömegű (vagy területű) részhez esik közelebb.

Tippek a pontosabb számításokhoz:

Mindig dolgozzunk egységes mértékegységekkel.
Ellenőrizzük, hogy a részek súlypontjai helyesen vannak-e meghatározva.
Szükség esetén használjunk szoftvert (pl. CAD programokat) a bonyolultabb alakzatok súlypontjának kiszámításához.
Tartsuk szem előtt, hogy a nem homogén testeknél külön kell kezelni az eltérő anyagokat, sűrűségeket.
Sose becsüljük alá a vázlatolás, szemléltetés jelentőségét!

További jó tanács:
Ha kétely merül fel, ellenőrizzük a végeredményt egyszerűbb módszerrel is (például egy „papírkivágós” modellel, ahol az egyensúlyi pontot kereshetjük meg fizikailag).

A súlypont meghatározása alapvető matematikai és fizikai képesség, amely nélkülözhetetlen a mérnöki, építészeti és művészeti munkák során is. Mint láttuk, az egyszerűbb alakzatoknál könnyen, szabályos képletekkel kiszámolható a súlypont, de összetettebb testek esetén a rész-alakzatos módszer vagy az integrálás válik szükségessé. Mindemellett fontos a precizitás, a helyes koordináta-választás, és hogy a kivágott, illetve hozzáadott részeket megfelelően vegyük figyelembe. A cikk célja, hogy segítséget adjon mindazoknak, akik akár hobbiként, akár hivatásszerűen foglalkoznak alakzatok súlypontjának meghatározásával; és bízunk benne, hogy a gyakorlati példák, tippek, illetve a GYIK rész is hozzájárult a téma elmélyítéséhez. Ne feledjük: a súlypont ismerete nem csupán elméleti tudás, hanem gyakorlati eszköz is, amely nélkülözhetetlen a stabilitás, az egyensúly és a biztonság szempontjából – legyen szó egy egyszerű rajzról, egy összetett műalkotásról vagy akár egy hatalmas építményről.

GYIK – Gyakran ismételt kérdések

1. Mi a különbség a súlypont és a tömegközéppont között?
A két fogalom a gyakorlatban gyakran szinonimaként szerepel. Ha az alakzat homogén anyagból van és egyenletes a sűrűsége, akkor a súlypont és a tömegközéppont egybeesik. Egyéb esetekben a tömegközéppont számításakor a tömegeloszlást is figyelembe kell venni.

2. Hogyan határozható meg a súlypont, ha az alakzatom anyaga nem homogén?
Ilyenkor minden rész tömegét és elhelyezkedését külön meg kell határozni, majd a súlyozott átlag képletét az egyes tömegekre alkalmazni.

3. Miért fontos a súlypont helyes meghatározása a mérnöki tervezés során?
A súlypont elhelyezkedése befolyásolja a szerkezet stabilitását, egyensúlyát, terhelését. Egy rosszul meghatározott súlypont veszélyt jelenthet (pl. felborulás, leszakadás).

4. Léteznek-e online kalkulátorok a súlypont számítására?
Igen, számos weboldal és program létezik, ahol különböző alakzatokhoz automatikusan kiszámolható a súlypont.

5. Mi a súlyvonal a háromszög esetén?
A súlyvonal a háromszög egyik csúcsát köti össze az ellentétes oldal felezőpontjával. A három súlyvonal metszéspontja lesz a háromszög súlypontja.

6. Hogy lehet ellenőrizni a számítás helyességét?
Készítsünk vázlatot, használjunk másik módszert is, vagy fizikailag is próbáljuk ki (például papírból kivágott alakzat egyensúlyi pontját keressük).

7. Mit tegyek, ha az alakzatom nem szabályos?
Bontsuk fel kisebb, szabályos részekre, vagy alkalmazzuk az integrálás módszerét.

8. Miért tolódik el a súlypont, ha lyuk van az alakzatban?
Mert a kivágott (hiányzó) rész súlya, tömege hiányzik, ezért a súlypont a megmaradó anyaghoz közelebb kerül.

9. Hogyan lehet gyorsan meghatározni egy szabályos sokszög súlypontját?
A szabályos sokszögek súlypontja mindig a középpontban van, amit a szimmetria miatt könnyű meghatározni.

10. Mi az integrálásos módszer fő előnye?
Bármilyen bonyolult vagy görbe alakzat esetén is alkalmazható, és a legpontosabb eredményt adja, bár matematikailag igényesebb.